Input interpretation

pressure of a column of fluid
Equation

P = ρ g h + P_0 | P | pressure at bottom of fluid column h | height of fluid column ρ | fluid density P_0 | pressure at top of fluid column g | standard acceleration due to gravity on the surface of the earth (≈ 9.807 m/s^2)
Units

Input values

height of fluid column | 0.3 meters fluid density | 1000 kg/m^3 (kilograms per cubic meter) pressure at top of fluid column | 100 kPa (kilopascals)
Results
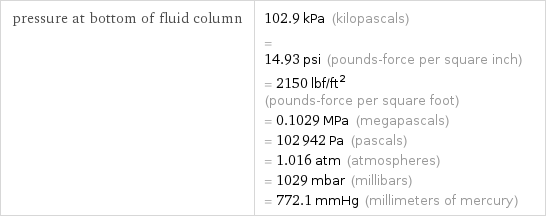
pressure at bottom of fluid column | 102.9 kPa (kilopascals) = 14.93 psi (pounds-force per square inch) = 2150 lbf/ft^2 (pounds-force per square foot) = 0.1029 MPa (megapascals) = 102942 Pa (pascals) = 1.016 atm (atmospheres) = 1029 mbar (millibars) = 772.1 mmHg (millimeters of mercury)
Possible intermediate steps

Calculate the pressure at bottom of fluid column using the following information: known variables | | h | height of fluid column | 0.3 m ρ | fluid density | 1000 kg/m^3 P_0 | pressure at top of fluid column | 100 kPa Convert known variables into appropriate units using the following: 1 kg/m^3 = 1000 g/m^3: 1 kPa = 1×10^6 g/(m s^2): known variables | | h | height of fluid column | 0.3 m ρ | fluid density | 1×10^6 g/m^3 P_0 | pressure at top of fluid column | 1×10^8 g/(m s^2) The relevant equation that relates pressure at bottom of fluid column (P), height of fluid column (h), fluid density (ρ), and pressure at top of fluid column (P_0) is: P = ρ g h + P_0 Substitute known variables and constants into the equation: known variables | | h | height of fluid column | 0.3 m ρ | fluid density | 1×10^6 g/m^3 P_0 | pressure at top of fluid column | 1×10^8 g/(m s^2) constant | | g | standard acceleration due to gravity on the surface of the earth | 196133/20000 m/s^2 | : P = 1×10^6 g/m^3×9.8067 m/s^2×0.3 m + 1×10^8 g/(m s^2) Separate the numerical part, 1×10^6×9.8067×0.3 + 1×10^8, from the unit part, g/m^3×m/s^2 m + g/(m s^2) = g/(m s^2): P = 1×10^6×9.8067×0.3 + 1×10^8 g/(m s^2) Evaluate 1×10^6×9.8067×0.3 + 1×10^8: P = 1.0294×10^8 g/(m s^2) Convert 1.0294×10^8 g/(m s^2) into kPa (kilopascals) using the following: 1 g/(m s^2) = 1×10^-6 kPa: Answer: | | P = 102.9 kPa