Input interpretation

Doppler shift
Equation

f_o/f_s = c/(c + v_s) | f_o/f_s | frequency reduction factor v_s | speed of the source away from the observer c | sound speed (the ratio between emitted and observed sound frequencies due to relative motion)
Input values

speed of the source away from the observer | 10 m/s (meters per second) sound speed | 340.27 m/s (meters per second)
Results

frequency reduction factor | 0.9715
Possible intermediate steps

Calculate the frequency reduction factor using the following information: known variables | | v_s | speed of the source away from the observer | 10 m/s c | sound speed | 340.27 m/s The relevant equation that relates frequency reduction factor (f_o/f_s), speed of the source away from the observer (v_s), and sound speed (c) is: f_o/f_s = c/(c + v_s) Substitute known variables into the equation: known variables | | v_s | speed of the source away from the observer | 10 m/s c | sound speed | 340.27 m/s | : f_o/f_s = (340.27 m/s)/(340.27 m/s + 10 m/s) Cancel the units in (340.27 m/s)/(340.27 m/s + 10 m/s): f_o/f_s = 340.27/(340.27 + 10) Evaluate 340.27/(340.27 + 10): Answer: | | f_o/f_s = 0.9715
Audible frequencies
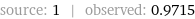
source: 1 | observed: 0.9715