Input interpretation
sulfur dioxide
Chemical names and formulas

formula | SO_2 Hill formula | O_2S name | sulfur dioxide alternate names | fermenicide liquid | fermenicide powder | Freon 764 | R-764 | sulfurous anhydride | sulfur oxide | sulphur dioxide mass fractions | O (oxygen) 50% | S (sulfur) 50%
Lewis structure

Draw the Lewis structure of sulfur dioxide. Start by drawing the overall structure of the molecule, ignoring potential double and triple bonds: Count the total valence electrons of the oxygen (n_O, val = 6) and sulfur (n_S, val = 6) atoms: 2 n_O, val + n_S, val = 18 Calculate the number of electrons needed to completely fill the valence shells for oxygen (n_O, full = 8) and sulfur (n_S, full = 8): 2 n_O, full + n_S, full = 24 Subtracting these two numbers shows that 24 - 18 = 6 bonding electrons are needed. Each bond has two electrons, so in addition to the 2 bonds already present in the diagram we expect to add 1 bond. To minimize formal charge oxygen wants 2 bonds. Identify the atoms that want additional bonds and the number of electrons remaining on each atom: Add 1 bond by pairing electrons between adjacent highlighted atoms. Additionally, atoms with large electronegativities can minimize their formal charge by forcing atoms with smaller electronegativities on period 3 or higher to expand their valence shells. The electronegativities of the atoms are 2.58 (sulfur) and 3.44 (oxygen). Because the electronegativity of sulfur is smaller than the electronegativity of oxygen, expand the valence shell of sulfur to 4 bonds. Therefore we add a total of 2 bonds to the diagram: Answer: | |
3D structure

3D structure
Basic properties
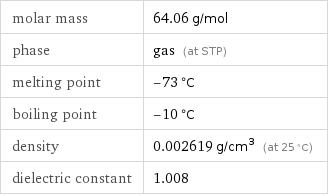
molar mass | 64.06 g/mol phase | gas (at STP) melting point | -73 °C boiling point | -10 °C density | 0.002619 g/cm^3 (at 25 °C) dielectric constant | 1.008
Gas properties (at STP)
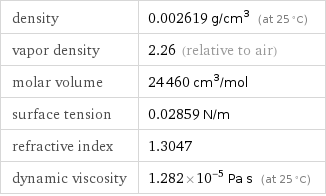
density | 0.002619 g/cm^3 (at 25 °C) vapor density | 2.26 (relative to air) molar volume | 24460 cm^3/mol surface tension | 0.02859 N/m refractive index | 1.3047 dynamic viscosity | 1.282×10^-5 Pa s (at 25 °C)
Units

Thermodynamic properties

specific heat capacity c_p | gas | 0.6229 J/(g K) molar heat capacity c_p | gas | 39.9 J/(mol K) specific free energy of formation Δ_fG° | gas | -4.685 kJ/g molar free energy of formation Δ_fG° | gas | -300.1 kJ/mol specific heat of formation Δ_fH° | gas | -4.633 kJ/g molar heat of formation Δ_fH° | gas | -296.8 kJ/mol specific entropy S° | gas | 3.871 J/(g K) molar entropy S° | gas | 248 J/(mol K) molar heat of vaporization | 25.4 kJ/mol | specific heat of vaporization | 0.397 kJ/g | molar heat of fusion | 8.6 kJ/mol | specific heat of fusion | 0.1343 kJ/g | thermal conductivity | 0.009743 W/(m K) | critical temperature | 430 K | critical pressure | 7.87 MPa | (at STP)
Phase diagram
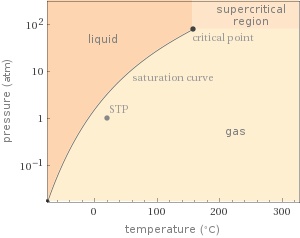
Phase diagram
Units
