Input interpretation

telescope light-gathering power ratio
Equation
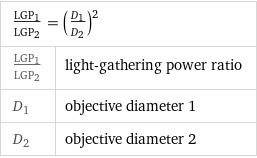
LGP_1/LGP_2 = (D_1/D_2)^2 | LGP_1/LGP_2 | light-gathering power ratio D_1 | objective diameter 1 D_2 | objective diameter 2
Input values

objective diameter 1 | 16 inches objective diameter 2 | 8 inches
Results

light-gathering power ratio | 4
Possible intermediate steps

Calculate the light-gathering power ratio using the following information: known variables | | D_1 | objective diameter 1 | 16 in D_2 | objective diameter 2 | 8 in The relevant equation that relates light-gathering power ratio (LGP_1/LGP_2), objective diameter 1 (D_1), and objective diameter 2 (D_2) is: LGP_1/LGP_2 = (D_1/D_2)^2 Substitute known variables into the equation: known variables | | D_1 | objective diameter 1 | 16 in D_2 | objective diameter 2 | 8 in | : LGP_1/LGP_2 = ((16 in)/(8 in))^2 Cancel the units in ((16 in)/(8 in))^2: LGP_1/LGP_2 = (16/8)^2 Evaluate (16/8)^2: Answer: | | LGP_1/LGP_2 = 4