Input interpretation

scandium(III) cation nickel(II) cation | coordination numbers
Result
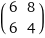
(6 | 8 6 | 4)
Characteristic polynomial
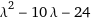
λ^2 - 10 λ - 24
Possible intermediate steps

Find the characteristic polynomial of the matrix M with respect to the variable λ: M = (6 | 8 6 | 4) To find the characteristic polynomial of a matrix, subtract a variable multiplied by the identity matrix and take the determinant: left bracketing bar M - λ I right bracketing bar left bracketing bar M - λ I right bracketing bar | = | left bracketing bar 6 | 8 6 | 4 - λ 1 | 0 0 | 1 right bracketing bar | = | left bracketing bar 6 | 8 6 | 4 - λ | 0 0 | λ right bracketing bar invisible comma = left bracketing bar 6 - λ | 8 6 | 4 - λ right bracketing bar Multiply along the diagonals and subtract: (6 - λ) (4 - λ) - 8 6 (6 - λ) (4 - λ) = λ^2 - 10 λ + 24: = 24 - 10 λ + λ^2 - 8 6 8×6 = 48: = (λ^2 - 10 λ + 24) - 48 (λ^2 - 10 λ + 24) - 48 = λ^2 - 10 λ - 24: Answer: | | = λ^2 - 10 λ - 24
Eigenvalues

λ_1 = 12

λ_2 = -2
Possible intermediate steps

Find all the eigenvalues of the matrix M: M = (6 | 8 6 | 4) Find λ element C such that M v = λ v for some nonzero vector v: M v = λ v Rewrite the equation M v = λ v as (M - I λ) v = 0: (M - I λ) v = 0 Find all λ such that left bracketing bar M - I λ right bracketing bar = 0: left bracketing bar M - I λ right bracketing bar = 0 M - I λ | = | (6 | 8 6 | 4) - (1 | 0 0 | 1) λ | = | (6 - λ | 8 6 | 4 - λ) invisible comma left bracketing bar 6 - λ | 8 6 | 4 - λ right bracketing bar = 0 left bracketing bar 6 - λ | 8 6 | 4 - λ right bracketing bar = λ^2 - 10 λ - 24: λ^2 - 10 λ - 24 = 0 The left hand side factors into a product with two terms: (λ - 12) (λ + 2) = 0 Split into two equations: λ - 12 = 0 or λ + 2 = 0 Add 12 to both sides: λ = 12 or λ + 2 = 0 Subtract 2 from both sides: Answer: | | λ = 12 or λ = -2
Eigenvectors

v_1 = (4, 3)

v_2 = (-1, 1)
Possible intermediate steps

Find all the eigenvalues and eigenvectors of the matrix M: M = (6 | 8 6 | 4) Find λ element C such that M v = λ v for some nonzero vector v: M v = λ v Rewrite the equation M v = λ v as (M - I λ) v = 0: (M - I λ) v = 0 Find all λ such that left bracketing bar M - I λ right bracketing bar = 0: left bracketing bar M - I λ right bracketing bar = 0 M - I λ | = | (6 | 8 6 | 4) - (1 | 0 0 | 1) λ | = | (6 - λ | 8 6 | 4 - λ) invisible comma left bracketing bar 6 - λ | 8 6 | 4 - λ right bracketing bar = 0 left bracketing bar 6 - λ | 8 6 | 4 - λ right bracketing bar = λ^2 - 10 λ - 24: λ^2 - 10 λ - 24 = 0 The left hand side factors into a product with two terms: (λ - 12) (λ + 2) = 0 Split into two equations: λ - 12 = 0 or λ + 2 = 0 Add 12 to both sides: λ = 12 or λ + 2 = 0 Subtract 2 from both sides: λ = 12 or λ = -2 Find all v such that (M - I λ) v = 0 for some eigenvalue λ: (M - I λ) v = 0 Substitute (6 - λ | 8 6 | 4 - λ) for (M - I λ): (6 - λ | 8 6 | 4 - λ) v = 0 Write v as (v_1 v_2) and 0 as (0 0): (6 - λ | 8 6 | 4 - λ).(v_1 v_2) = (0 0) First, substitute 12 for λ in the matrix (6 - λ | 8 6 | 4 - λ) and solve the system: (-6 | 8 6 | -8).(v_1 v_2) = (0 0) In augmented matrix form, the system is written as: (-6 | 8 | 0 6 | -8 | 0) Add row 1 to row 2: (-6 | 8 | 0 0 | 0 | 0) Divide row 1 by -6: (1 | -4/3 | 0 0 | 0 | 0) Translated back to a matrix equation, the reduced system (1 | -4/3 | 0 0 | 0 | 0) is: (1 | -4/3 0 | 0)(v_1 v_2) = (0 0) As a scalar equation, the system (1 | -4/3 0 | 0)(v_1 v_2) = (0 0) translates to: v_1 - (4 v_2)/3 = 0 Rewrite the equation as: v_1 = (4 v_2)/3 According to the above equation: v = (v_1 v_2) = ((4 v_2)/3 v_2) Letting v_2 = 1 in ((4 v_2)/3 v_2), we find that (4/3 1) is an eigenvector of the matrix (6 | 8 6 | 4) associated with the eigenvalue 12: v = (4/3 1) Substitute -2 for λ in the matrix (6 - λ | 8 6 | 4 - λ) and solve the system: (8 | 8 6 | 6).(v_1 v_2) = (0 0) In augmented matrix form, the system is written as: (8 | 8 | 0 6 | 6 | 0) Subtract 3/4 × (row 1) from row 2: (8 | 8 | 0 0 | 0 | 0) Divide row 1 by 8: (1 | 1 | 0 0 | 0 | 0) Translated back to a matrix equation, the reduced system (1 | 1 | 0 0 | 0 | 0) is: (1 | 1 0 | 0)(v_1 v_2) = (0 0) As a scalar equation, the system (1 | 1 0 | 0)(v_1 v_2) = (0 0) translates to: v_1 + v_2 = 0 Rewrite the equation as: v_1 = -v_2 According to the above equation: v = (v_1 v_2) = (-v_2 v_2) Letting v_2 = 1 in (-v_2 v_2), we find that (-1 1) is an eigenvector of the matrix (6 | 8 6 | 4) associated with the eigenvalue -2: v = (-1 1) We found the following eigenvalue/eigenvector pair: Answer: | | Eigenvalue | Eigenvector 12 | (4/3 1) -2 | (-1 1)
Diagonalization
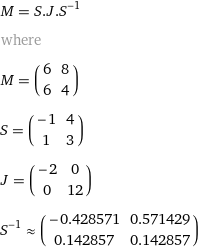
M = S.J.S^(-1) where M = (6 | 8 6 | 4) S = (-1 | 4 1 | 3) J = (-2 | 0 0 | 12) S^(-1)≈(-0.428571 | 0.571429 0.142857 | 0.142857)