Input interpretation
destructive thin film interference
Equation

2 t = (m λ n_1)/n_2 | λ | wavelength for destructive interference t | thickness m | order n_1 | index of refraction of outside medium n_2 | index of refraction of thin film
Input values
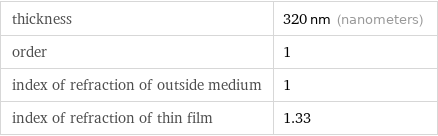
thickness | 320 nm (nanometers) order | 1 index of refraction of outside medium | 1 index of refraction of thin film | 1.33
Results

wavelength for destructive interference | 851.2 nm (nanometers) = 3.351×10^-5 inches = 0.8512 µm (micrometers) = 8.512×10^-7 meters
Possible intermediate steps

Calculate the wavelength for destructive interference using the following information: known variables | | t | thickness | 320 nm m | order | 1 n_1 | index of refraction of outside medium | 1 n_2 | index of refraction of thin film | 1.33 The relevant equation that relates wavelength for destructive interference (λ), thickness (t), order (m), index of refraction of outside medium (n_1), and index of refraction of thin film (n_2) is: 2 t = (m λ n_1)/n_2 t×2 = (m λ n_1)/n_2 is equivalent to (m λ n_1)/n_2 = t×2: (m λ n_1)/n_2 = t 2 Divide both sides by (m n_1)/n_2: λ = (t n_2 2)/(m n_1) Substitute known variables into the equation: known variables | | t | thickness | 320 nm m | order | 1 n_1 | index of refraction of outside medium | 1 n_2 | index of refraction of thin film | 1.33 | : λ = 1.33×320 nm×2 Separate the numerical part, 1.33×320×2, from the unit part, nm: λ = 1.33×320×2 nm Evaluate 1.33×320×2: Answer: | | λ = 851.2 nm