Input interpretation

trimethylamine | phase | gas
Thermodynamic properties of matter
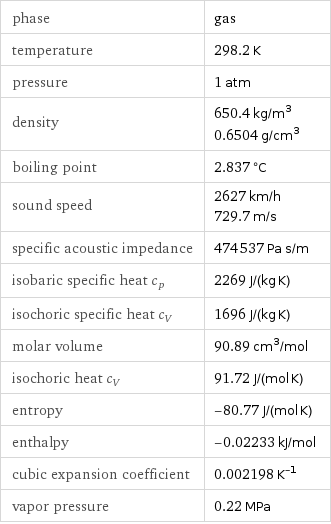
phase | gas temperature | 298.2 K pressure | 1 atm density | 650.4 kg/m^3 0.6504 g/cm^3 boiling point | 2.837 °C sound speed | 2627 km/h 729.7 m/s specific acoustic impedance | 474537 Pa s/m isobaric specific heat c_p | 2269 J/(kg K) isochoric specific heat c_V | 1696 J/(kg K) molar volume | 90.89 cm^3/mol isochoric heat c_V | 91.72 J/(mol K) entropy | -80.77 J/(mol K) enthalpy | -0.02233 kJ/mol cubic expansion coefficient | 0.002198 K^(-1) vapor pressure | 0.22 MPa
Lewis structure

Draw the Lewis structure of trimethylamine. Start by drawing the overall structure of the molecule: Count the total valence electrons of the carbon (n_C, val = 4), hydrogen (n_H, val = 1), and nitrogen (n_N, val = 5) atoms: 3 n_C, val + 9 n_H, val + n_N, val = 26 Calculate the number of electrons needed to completely fill the valence shells for carbon (n_C, full = 8), hydrogen (n_H, full = 2), and nitrogen (n_N, full = 8): 3 n_C, full + 9 n_H, full + n_N, full = 50 Subtracting these two numbers shows that 50 - 26 = 24 bonding electrons are needed. Each bond has two electrons, so the above diagram has all the necessary bonds. There are 12 bonds and hence 24 bonding electrons in the diagram. Lastly, fill in the remaining unbonded electrons on each atom. In total, there remain 26 - 24 = 2 electrons left to draw: Answer: | |
3D structure
3D structure
Basic properties
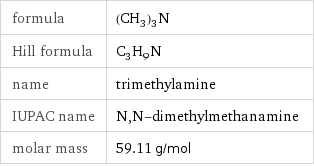
formula | (CH_3)_3N Hill formula | C_3H_9N name | trimethylamine IUPAC name | N, N-dimethylmethanamine molar mass | 59.11 g/mol
Units
