Input interpretation
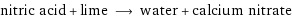
nitric acid + lime ⟶ water + calcium nitrate
Balanced equation

Balance the chemical equation algebraically: + ⟶ + Add stoichiometric coefficients, c_i, to the reactants and products: c_1 + c_2 ⟶ c_3 + c_4 Set the number of atoms in the reactants equal to the number of atoms in the products for H, N, O and Ca: H: | c_1 = 2 c_3 N: | c_1 = 2 c_4 O: | 3 c_1 + c_2 = c_3 + 6 c_4 Ca: | c_2 = c_4 Since the coefficients are relative quantities and underdetermined, choose a coefficient to set arbitrarily. To keep the coefficients small, the arbitrary value is ordinarily one. For instance, set c_2 = 1 and solve the system of equations for the remaining coefficients: c_1 = 2 c_2 = 1 c_3 = 1 c_4 = 1 Substitute the coefficients into the chemical reaction to obtain the balanced equation: Answer: | | 2 + ⟶ +
Structures
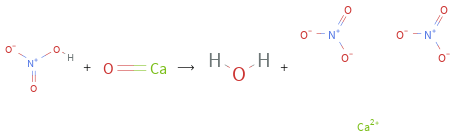
+ ⟶ +
Names
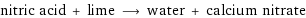
nitric acid + lime ⟶ water + calcium nitrate
Reaction thermodynamics
Gibbs free energy
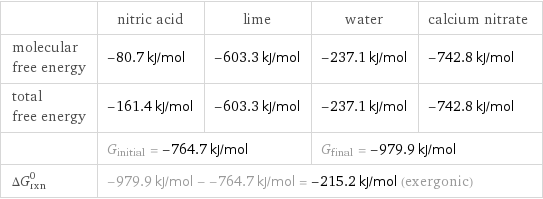
| nitric acid | lime | water | calcium nitrate molecular free energy | -80.7 kJ/mol | -603.3 kJ/mol | -237.1 kJ/mol | -742.8 kJ/mol total free energy | -161.4 kJ/mol | -603.3 kJ/mol | -237.1 kJ/mol | -742.8 kJ/mol | G_initial = -764.7 kJ/mol | | G_final = -979.9 kJ/mol | ΔG_rxn^0 | -979.9 kJ/mol - -764.7 kJ/mol = -215.2 kJ/mol (exergonic) | | |
Chemical names and formulas
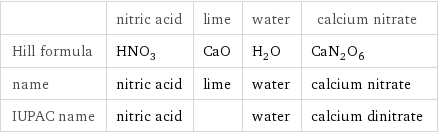
| nitric acid | lime | water | calcium nitrate Hill formula | HNO_3 | CaO | H_2O | CaN_2O_6 name | nitric acid | lime | water | calcium nitrate IUPAC name | nitric acid | | water | calcium dinitrate
Substance properties
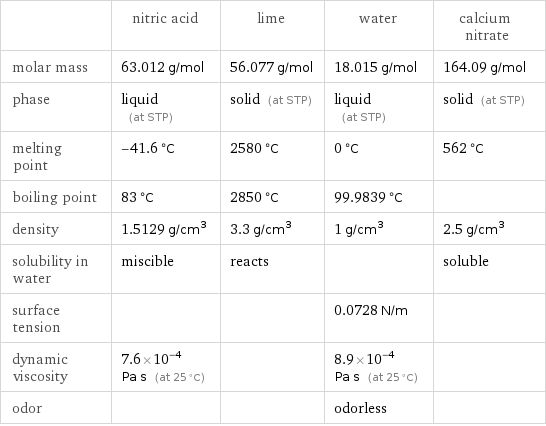
| nitric acid | lime | water | calcium nitrate molar mass | 63.012 g/mol | 56.077 g/mol | 18.015 g/mol | 164.09 g/mol phase | liquid (at STP) | solid (at STP) | liquid (at STP) | solid (at STP) melting point | -41.6 °C | 2580 °C | 0 °C | 562 °C boiling point | 83 °C | 2850 °C | 99.9839 °C | density | 1.5129 g/cm^3 | 3.3 g/cm^3 | 1 g/cm^3 | 2.5 g/cm^3 solubility in water | miscible | reacts | | soluble surface tension | | | 0.0728 N/m | dynamic viscosity | 7.6×10^-4 Pa s (at 25 °C) | | 8.9×10^-4 Pa s (at 25 °C) | odor | | | odorless |
Units
