Input interpretation

palladium(II) ions | formal charges
Result
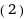
(2)
Table
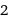
2
Characteristic polynomial
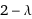
2 - λ
Possible intermediate steps

Find the characteristic polynomial of the matrix M with respect to the variable λ: M = (2) To find the characteristic polynomial of a matrix, subtract a variable multiplied by the identity matrix and take the determinant: left bracketing bar M - λ I right bracketing bar left bracketing bar M - λ I right bracketing bar | = | left bracketing bar 2 - λ 1 right bracketing bar | = | left bracketing bar 2 - λ right bracketing bar invisible comma = left bracketing bar 2 - λ right bracketing bar The determinant of a diagonal matrix is the product of its diagonal elements: left bracketing bar 2 - λ right bracketing bar 2 - λ = 2 - λ: Answer: | | 2 - λ
Eigenvalues

λ_1 = 2
Possible intermediate steps

Find all the eigenvalues of the matrix M: M = (2) Find λ element C such that M v = λ v for some nonzero vector v: M v = λ v The only value of λ for which M v = λ v for any nonzero v is 2: Answer: | | 2
Eigenvectors

v_1 = (1)
Possible intermediate steps

Find all the eigenvalues and eigenvectors of the matrix M: M = (2) Find λ element C such that M v = λ v for some nonzero vector v: M v = λ v The only value of λ for which M v = λ v for any nonzero v is 2: 2 The equation M v = λ v is satisfied by each v element C^1, which means a suitable eigenvalue/eigenvector pair is: Answer: | | Eigenvalue | Eigenvector 2 | (1)