Input interpretation
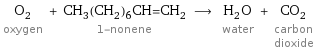
O_2 oxygen + CH_3(CH_2)_6CH=CH_2 1-nonene ⟶ H_2O water + CO_2 carbon dioxide
Balanced equation

Balance the chemical equation algebraically: O_2 + CH_3(CH_2)_6CH=CH_2 ⟶ H_2O + CO_2 Add stoichiometric coefficients, c_i, to the reactants and products: c_1 O_2 + c_2 CH_3(CH_2)_6CH=CH_2 ⟶ c_3 H_2O + c_4 CO_2 Set the number of atoms in the reactants equal to the number of atoms in the products for O, C and H: O: | 2 c_1 = c_3 + 2 c_4 C: | 9 c_2 = c_4 H: | 18 c_2 = 2 c_3 Since the coefficients are relative quantities and underdetermined, choose a coefficient to set arbitrarily. To keep the coefficients small, the arbitrary value is ordinarily one. For instance, set c_2 = 1 and solve the system of equations for the remaining coefficients: c_1 = 27/2 c_2 = 1 c_3 = 9 c_4 = 9 Multiply by the least common denominator, 2, to eliminate fractional coefficients: c_1 = 27 c_2 = 2 c_3 = 18 c_4 = 18 Substitute the coefficients into the chemical reaction to obtain the balanced equation: Answer: | | 27 O_2 + 2 CH_3(CH_2)_6CH=CH_2 ⟶ 18 H_2O + 18 CO_2
Structures
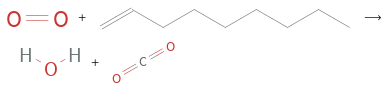
+ ⟶ +
Names
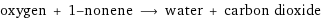
oxygen + 1-nonene ⟶ water + carbon dioxide
Equilibrium constant
![K_c = ([H2O]^18 [CO2]^18)/([O2]^27 [CH3(CH2)6CH=CH2]^2)](../image_source/66928ff50a737022e5844596aee6c507.png)
K_c = ([H2O]^18 [CO2]^18)/([O2]^27 [CH3(CH2)6CH=CH2]^2)
Rate of reaction
![rate = -1/27 (Δ[O2])/(Δt) = -1/2 (Δ[CH3(CH2)6CH=CH2])/(Δt) = 1/18 (Δ[H2O])/(Δt) = 1/18 (Δ[CO2])/(Δt) (assuming constant volume and no accumulation of intermediates or side products)](../image_source/78d39ba9f2fd28e009c3335e29ab99f0.png)
rate = -1/27 (Δ[O2])/(Δt) = -1/2 (Δ[CH3(CH2)6CH=CH2])/(Δt) = 1/18 (Δ[H2O])/(Δt) = 1/18 (Δ[CO2])/(Δt) (assuming constant volume and no accumulation of intermediates or side products)
Chemical names and formulas
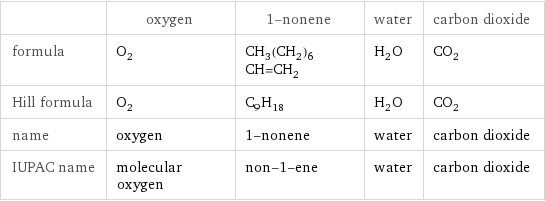
| oxygen | 1-nonene | water | carbon dioxide formula | O_2 | CH_3(CH_2)_6CH=CH_2 | H_2O | CO_2 Hill formula | O_2 | C_9H_18 | H_2O | CO_2 name | oxygen | 1-nonene | water | carbon dioxide IUPAC name | molecular oxygen | non-1-ene | water | carbon dioxide