Input interpretation

diffraction grating
Equation

d sin(θ_m) = m λ | θ_m | diffraction angle d | slit separation distance λ | wavelength m | diffraction order
Input values
slit separation distance | 0.1 mm (millimeters) wavelength | 500 nm (nanometers) diffraction order | 1
Results

diffraction angle | 0.2865° (degrees) = 5 mrad (milliradians) = 0.005 radians = 17 arc minutes 11.33 arc seconds = 17.19' (arc minutes)
Possible intermediate steps

Calculate the diffraction angle using the following information: known variables | | d | slit separation distance | 0.1 mm λ | wavelength | 500 nm m | diffraction order | 1 Convert known variables into appropriate units using the following: 1 mm = 0.001 m: 1 nm = 1×10^-9 m: known variables | | d | slit separation distance | 1×10^-4 m λ | wavelength | 1/2000000 m m | diffraction order | 1 The relevant equation that relates diffraction angle (θ_m), slit separation distance (d), wavelength (λ), and diffraction order (m) is: d sin(θ_m) = m λ Divide both sides by d: sin(θ_m) = (m λ)/d Take the inverse sine of both sides: θ_m = sin^(-1)((m λ)/d) Substitute known variables into the equation: known variables | | d | slit separation distance | 1×10^-4 m λ | wavelength | 1/2000000 m m | diffraction order | 1 | : θ_m = sin^(-1)((5×10^-7 m)/(1×10^-4 m)) Cancel any units in sin^(-1)((5×10^-7 m)/(1×10^-4 m)) and add the unit rad for angles: θ_m = sin^(-1)((5×10^-7)/(1×10^-4)) rad Evaluate sin^(-1)((5×10^-7)/(1×10^-4)): θ_m = 0.005 rad Convert 0.005 rad into degrees using the following: 1 rad = 57.296°: Answer: | | θ_m = 0.2865°
Normalized transmitted intensity vs. diffraction angle
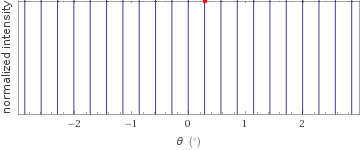
Normalized transmitted intensity vs. diffraction angle