Input interpretation
ammonia + methanol ⟶ water + methylamine
Balanced equation

Balance the chemical equation algebraically: + ⟶ + Add stoichiometric coefficients, c_i, to the reactants and products: c_1 + c_2 ⟶ c_3 + c_4 Set the number of atoms in the reactants equal to the number of atoms in the products for H, N, C and O: H: | 3 c_1 + 4 c_2 = 2 c_3 + 5 c_4 N: | c_1 = c_4 C: | c_2 = c_4 O: | c_2 = c_3 Since the coefficients are relative quantities and underdetermined, choose a coefficient to set arbitrarily. To keep the coefficients small, the arbitrary value is ordinarily one. For instance, set c_1 = 1 and solve the system of equations for the remaining coefficients: c_1 = 1 c_2 = 1 c_3 = 1 c_4 = 1 Substitute the coefficients into the chemical reaction to obtain the balanced equation: Answer: | | + ⟶ +
Structures
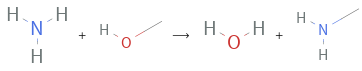
+ ⟶ +
Names
ammonia + methanol ⟶ water + methylamine
Reaction thermodynamics
Enthalpy
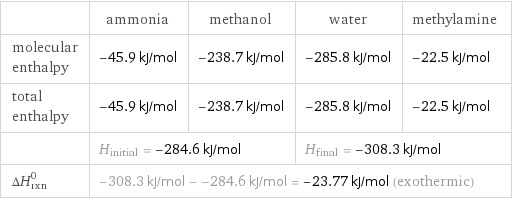
| ammonia | methanol | water | methylamine molecular enthalpy | -45.9 kJ/mol | -238.7 kJ/mol | -285.8 kJ/mol | -22.5 kJ/mol total enthalpy | -45.9 kJ/mol | -238.7 kJ/mol | -285.8 kJ/mol | -22.5 kJ/mol | H_initial = -284.6 kJ/mol | | H_final = -308.3 kJ/mol | ΔH_rxn^0 | -308.3 kJ/mol - -284.6 kJ/mol = -23.77 kJ/mol (exothermic) | | |
Chemical names and formulas
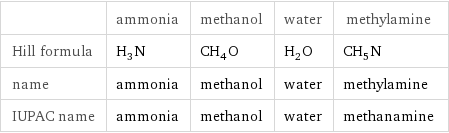
| ammonia | methanol | water | methylamine Hill formula | H_3N | CH_4O | H_2O | CH_5N name | ammonia | methanol | water | methylamine IUPAC name | ammonia | methanol | water | methanamine