Input interpretation
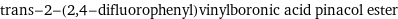
trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester
Basic properties

molar mass | 266.1 g/mol formula | C_14H_17BF_2O_2 empirical formula | F_2C_14B_O_2H_17 SMILES identifier | CC1(C)C(C)(C)OB(/C=C/C2=C(C=C(C=C2)F)F)O1 InChI identifier | InChI=1/C14H17BF2O2/c1-13(2)14(3, 4)19-15(18-13)8-7-10-5-6-11(16)9-12(10)17/h5-9H, 1-4H3/b8-7+ InChI key | BMZXZTQQERUFEM-BQYQJAHWSA-N
Lewis structure
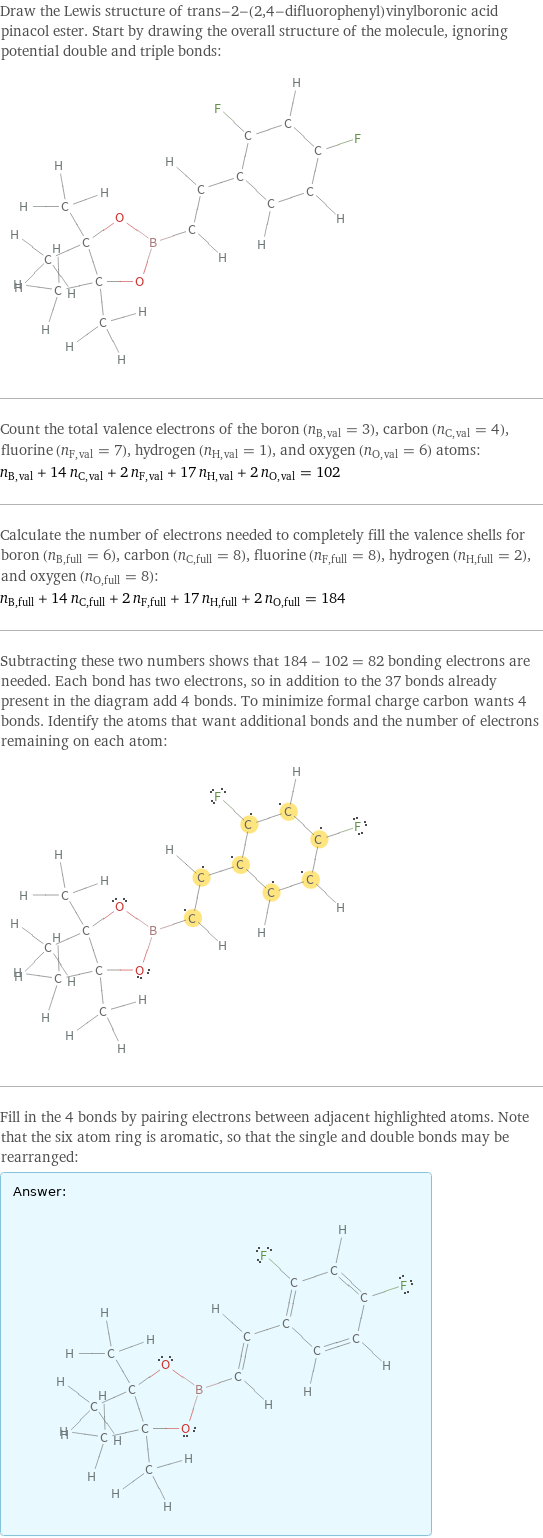
Draw the Lewis structure of trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester. Start by drawing the overall structure of the molecule, ignoring potential double and triple bonds: Count the total valence electrons of the boron (n_B, val = 3), carbon (n_C, val = 4), fluorine (n_F, val = 7), hydrogen (n_H, val = 1), and oxygen (n_O, val = 6) atoms: n_B, val + 14 n_C, val + 2 n_F, val + 17 n_H, val + 2 n_O, val = 102 Calculate the number of electrons needed to completely fill the valence shells for boron (n_B, full = 6), carbon (n_C, full = 8), fluorine (n_F, full = 8), hydrogen (n_H, full = 2), and oxygen (n_O, full = 8): n_B, full + 14 n_C, full + 2 n_F, full + 17 n_H, full + 2 n_O, full = 184 Subtracting these two numbers shows that 184 - 102 = 82 bonding electrons are needed. Each bond has two electrons, so in addition to the 37 bonds already present in the diagram add 4 bonds. To minimize formal charge carbon wants 4 bonds. Identify the atoms that want additional bonds and the number of electrons remaining on each atom: Fill in the 4 bonds by pairing electrons between adjacent highlighted atoms. Note that the six atom ring is aromatic, so that the single and double bonds may be rearranged: Answer: | |
Quantitative molecular descriptors
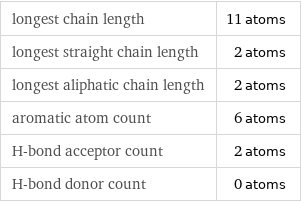
longest chain length | 11 atoms longest straight chain length | 2 atoms longest aliphatic chain length | 2 atoms aromatic atom count | 6 atoms H-bond acceptor count | 2 atoms H-bond donor count | 0 atoms
Elemental composition

Find the elemental composition for trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester in terms of the atom and mass percents: atom percent = N_i/N_atoms × 100% mass percent = (N_im_i)/m × 100% Plan: • Write the chemical formula and gather atomic masses from the periodic table. • Determine values for N_i, m_i, N_atoms and m using these items. • Finally, compute the percents and check the results. Write the chemical formula: C_14H_17BF_2O_2 Use the chemical formula, C_14H_17BF_2O_2, to count the number of atoms, N_i, for each element and find the total number of atoms, N_atoms: | number of atoms F (fluorine) | 2 C (carbon) | 14 B (boron) | 1 O (oxygen) | 2 H (hydrogen) | 17 N_atoms = 2 + 14 + 1 + 2 + 17 = 36 Divide each N_i by N_atoms to calculate atom fractions. Then use the property that atom fractions must sum to one to check the work: | number of atoms | atom fraction F (fluorine) | 2 | 2/36 C (carbon) | 14 | 14/36 B (boron) | 1 | 1/36 O (oxygen) | 2 | 2/36 H (hydrogen) | 17 | 17/36 Check: 2/36 + 14/36 + 1/36 + 2/36 + 17/36 = 1 Compute atom percents using the atom fractions: | number of atoms | atom percent F (fluorine) | 2 | 2/36 × 100% = 5.56% C (carbon) | 14 | 14/36 × 100% = 38.9% B (boron) | 1 | 1/36 × 100% = 2.78% O (oxygen) | 2 | 2/36 × 100% = 5.56% H (hydrogen) | 17 | 17/36 × 100% = 47.2% Look up the atomic mass, m_i, in unified atomic mass units, u, for each element in the periodic table: | number of atoms | atom percent | atomic mass/u F (fluorine) | 2 | 5.56% | 18.998403163 C (carbon) | 14 | 38.9% | 12.011 B (boron) | 1 | 2.78% | 10.81 O (oxygen) | 2 | 5.56% | 15.999 H (hydrogen) | 17 | 47.2% | 1.008 Multiply N_i by m_i to compute the mass for each element. Then sum those values to compute the molecular mass, m: | number of atoms | atom percent | atomic mass/u | mass/u F (fluorine) | 2 | 5.56% | 18.998403163 | 2 × 18.998403163 = 37.996806326 C (carbon) | 14 | 38.9% | 12.011 | 14 × 12.011 = 168.154 B (boron) | 1 | 2.78% | 10.81 | 1 × 10.81 = 10.81 O (oxygen) | 2 | 5.56% | 15.999 | 2 × 15.999 = 31.998 H (hydrogen) | 17 | 47.2% | 1.008 | 17 × 1.008 = 17.136 m = 37.996806326 u + 168.154 u + 10.81 u + 31.998 u + 17.136 u = 266.094806326 u Divide the mass for each element by m to calculate mass fractions. Then use the property that mass fractions must sum to one to check the work: | number of atoms | atom percent | mass fraction F (fluorine) | 2 | 5.56% | 37.996806326/266.094806326 C (carbon) | 14 | 38.9% | 168.154/266.094806326 B (boron) | 1 | 2.78% | 10.81/266.094806326 O (oxygen) | 2 | 5.56% | 31.998/266.094806326 H (hydrogen) | 17 | 47.2% | 17.136/266.094806326 Check: 37.996806326/266.094806326 + 168.154/266.094806326 + 10.81/266.094806326 + 31.998/266.094806326 + 17.136/266.094806326 = 1 Compute mass percents using the mass fractions: Answer: | | | number of atoms | atom percent | mass percent F (fluorine) | 2 | 5.56% | 37.996806326/266.094806326 × 100% = 14.28% C (carbon) | 14 | 38.9% | 168.154/266.094806326 × 100% = 63.19% B (boron) | 1 | 2.78% | 10.81/266.094806326 × 100% = 4.062% O (oxygen) | 2 | 5.56% | 31.998/266.094806326 × 100% = 12.03% H (hydrogen) | 17 | 47.2% | 17.136/266.094806326 × 100% = 6.440%
Elemental oxidation states

The first step in finding the oxidation states (or oxidation numbers) in trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester is to draw the structure diagram. Next set every oxidation number equal to the atom's formal charge: In trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester hydrogen is not bonded to a metal with lower electronegativity, so it will have an oxidation state of +1. Any element bonded to hydrogen gains the bonding electrons, decreasing their oxidation state by 1 for every bond: With hydrogen out of the way, look at the remaining bonds. There are 1 boron-carbon bond, 2 boron-oxygen bonds, 2 carbon-fluorine bonds, 2 carbon-oxygen bonds, and 13 carbon-carbon bonds. For each of these bonds, assign the bonding electrons to the most electronegative element. First examine the boron-carbon bond: element | electronegativity (Pauling scale) | B | 2.04 | C | 2.55 | | | Since carbon is more electronegative than boron, the electrons in this bond will go to carbon. Decrease the oxidation number for carbon (by 1 for single bonds, 2 for double bonds, and 3 for triple bonds), and increase the oxidation number for boron accordingly: Next look at the boron-oxygen bonds: element | electronegativity (Pauling scale) | B | 2.04 | O | 3.44 | | | Since oxygen is more electronegative than boron, the electrons in these bonds will go to oxygen: Next look at the carbon-fluorine bonds: element | electronegativity (Pauling scale) | C | 2.55 | F | 3.98 | | | Since fluorine is more electronegative than carbon, the electrons in these bonds will go to fluorine: Next look at the carbon-oxygen bonds: element | electronegativity (Pauling scale) | C | 2.55 | O | 3.44 | | | Since oxygen is more electronegative than carbon, the electrons in these bonds will go to oxygen: Next look at the carbon-carbon bonds: element | electronegativity (Pauling scale) | C | 2.55 | C | 2.55 | | | Since these elements are the same the bonding electrons are shared equally, and there is no change to the oxidation states: Now summarize the results: Answer: | | oxidation state | element | count -3 | C (carbon) | 4 -2 | C (carbon) | 1 | O (oxygen) | 2 -1 | C (carbon) | 4 | F (fluorine) | 2 0 | C (carbon) | 1 +1 | C (carbon) | 4 | H (hydrogen) | 17 +3 | B (boron) | 1
Orbital hybridization
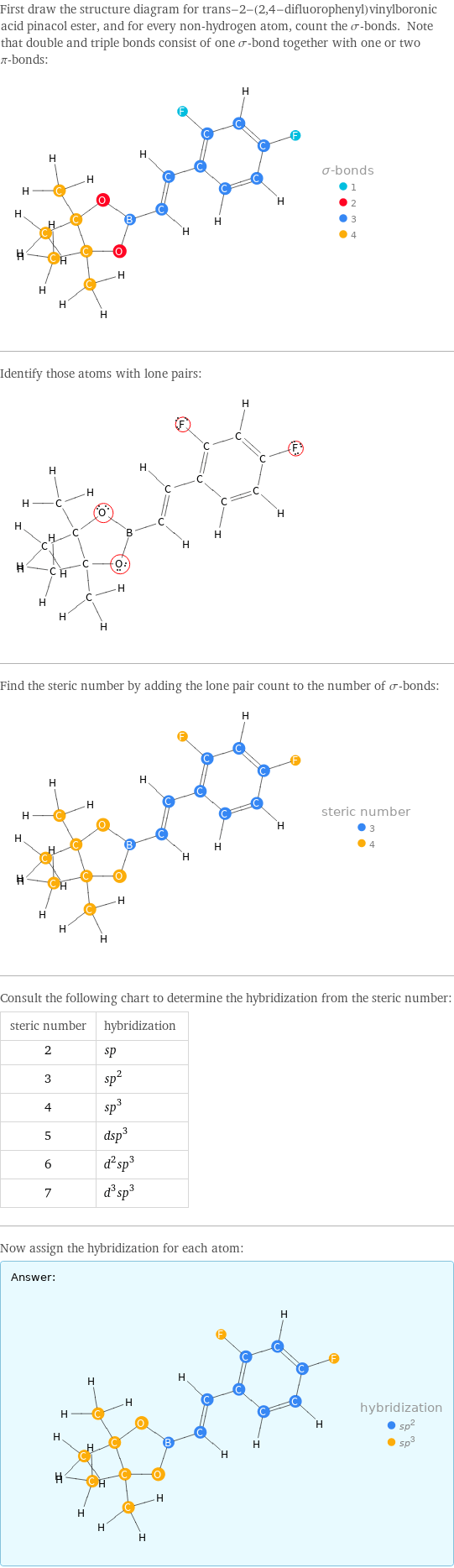
First draw the structure diagram for trans-2-(2, 4-difluorophenyl)vinylboronic acid pinacol ester, and for every non-hydrogen atom, count the σ-bonds. Note that double and triple bonds consist of one σ-bond together with one or two π-bonds: Identify those atoms with lone pairs: Find the steric number by adding the lone pair count to the number of σ-bonds: Consult the following chart to determine the hybridization from the steric number: steric number | hybridization 2 | sp 3 | sp^2 4 | sp^3 5 | dsp^3 6 | d^2sp^3 7 | d^3sp^3 Now assign the hybridization for each atom: Answer: | |
Topological indices
vertex count | 36 edge count | 37 Schultz index | 13140 Wiener index | 3351 Hosoya index | 3.95×10^6 Balaban index | 2.691