Input interpretation

Arrhenius bases | molar mass
Summary
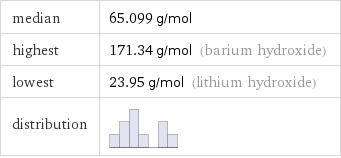
median | 65.099 g/mol highest | 171.34 g/mol (barium hydroxide) lowest | 23.95 g/mol (lithium hydroxide) distribution |
Units

Distribution plots
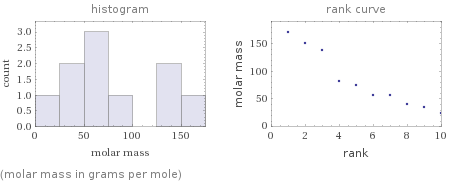
(molar mass in grams per mole)
Molar mass rankings
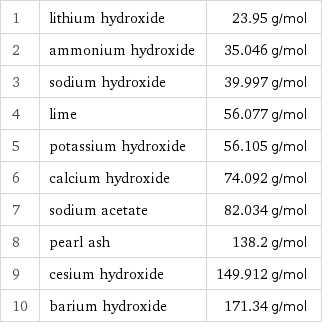
1 | lithium hydroxide | 23.95 g/mol 2 | ammonium hydroxide | 35.046 g/mol 3 | sodium hydroxide | 39.997 g/mol 4 | lime | 56.077 g/mol 5 | potassium hydroxide | 56.105 g/mol 6 | calcium hydroxide | 74.092 g/mol 7 | sodium acetate | 82.034 g/mol 8 | pearl ash | 138.2 g/mol 9 | cesium hydroxide | 149.912 g/mol 10 | barium hydroxide | 171.34 g/mol
Unit conversion for median molar mass 65.099 g/mol
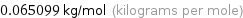
0.065099 kg/mol (kilograms per mole)
Comparisons for median molar mass 65.099 g/mol

≈ ( 0.09 ≈ 1/11 ) × molar mass of fullerene (≈ 721 g/mol )
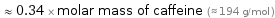
≈ 0.34 × molar mass of caffeine (≈ 194 g/mol )
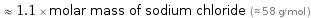
≈ 1.1 × molar mass of sodium chloride (≈ 58 g/mol )
Corresponding quantities
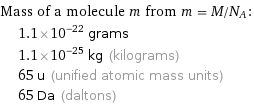
Mass of a molecule m from m = M/N_A: | 1.1×10^-22 grams | 1.1×10^-25 kg (kilograms) | 65 u (unified atomic mass units) | 65 Da (daltons)
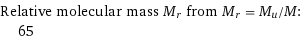
Relative molecular mass M_r from M_r = M_u/M: | 65