Input interpretation
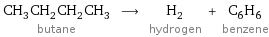
CH_3CH_2CH_2CH_3 butane ⟶ H_2 hydrogen + C_6H_6 benzene
Balanced equation

Balance the chemical equation algebraically: CH_3CH_2CH_2CH_3 ⟶ H_2 + C_6H_6 Add stoichiometric coefficients, c_i, to the reactants and products: c_1 CH_3CH_2CH_2CH_3 ⟶ c_2 H_2 + c_3 C_6H_6 Set the number of atoms in the reactants equal to the number of atoms in the products for C and H: C: | 4 c_1 = 6 c_3 H: | 10 c_1 = 2 c_2 + 6 c_3 Since the coefficients are relative quantities and underdetermined, choose a coefficient to set arbitrarily. To keep the coefficients small, the arbitrary value is ordinarily one. For instance, set c_3 = 1 and solve the system of equations for the remaining coefficients: c_1 = 3/2 c_2 = 9/2 c_3 = 1 Multiply by the least common denominator, 2, to eliminate fractional coefficients: c_1 = 3 c_2 = 9 c_3 = 2 Substitute the coefficients into the chemical reaction to obtain the balanced equation: Answer: | | 3 CH_3CH_2CH_2CH_3 ⟶ 9 H_2 + 2 C_6H_6
Structures
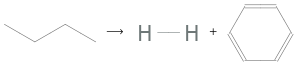
⟶ +
Names
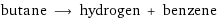
butane ⟶ hydrogen + benzene
Equilibrium constant
![Construct the equilibrium constant, K, expression for: CH_3CH_2CH_2CH_3 ⟶ H_2 + C_6H_6 Plan: • Balance the chemical equation. • Determine the stoichiometric numbers. • Assemble the activity expression for each chemical species. • Use the activity expressions to build the equilibrium constant expression. Write the balanced chemical equation: 3 CH_3CH_2CH_2CH_3 ⟶ 9 H_2 + 2 C_6H_6 Assign stoichiometric numbers, ν_i, using the stoichiometric coefficients, c_i, from the balanced chemical equation in the following manner: ν_i = -c_i for reactants and ν_i = c_i for products: chemical species | c_i | ν_i CH_3CH_2CH_2CH_3 | 3 | -3 H_2 | 9 | 9 C_6H_6 | 2 | 2 Assemble the activity expressions accounting for the state of matter and ν_i: chemical species | c_i | ν_i | activity expression CH_3CH_2CH_2CH_3 | 3 | -3 | ([CH3CH2CH2CH3])^(-3) H_2 | 9 | 9 | ([H2])^9 C_6H_6 | 2 | 2 | ([C6H6])^2 The equilibrium constant symbol in the concentration basis is: K_c Mulitply the activity expressions to arrive at the K_c expression: Answer: | | K_c = ([CH3CH2CH2CH3])^(-3) ([H2])^9 ([C6H6])^2 = (([H2])^9 ([C6H6])^2)/([CH3CH2CH2CH3])^3](../image_source/cb203b6319e480250408625d321f0258.png)
Construct the equilibrium constant, K, expression for: CH_3CH_2CH_2CH_3 ⟶ H_2 + C_6H_6 Plan: • Balance the chemical equation. • Determine the stoichiometric numbers. • Assemble the activity expression for each chemical species. • Use the activity expressions to build the equilibrium constant expression. Write the balanced chemical equation: 3 CH_3CH_2CH_2CH_3 ⟶ 9 H_2 + 2 C_6H_6 Assign stoichiometric numbers, ν_i, using the stoichiometric coefficients, c_i, from the balanced chemical equation in the following manner: ν_i = -c_i for reactants and ν_i = c_i for products: chemical species | c_i | ν_i CH_3CH_2CH_2CH_3 | 3 | -3 H_2 | 9 | 9 C_6H_6 | 2 | 2 Assemble the activity expressions accounting for the state of matter and ν_i: chemical species | c_i | ν_i | activity expression CH_3CH_2CH_2CH_3 | 3 | -3 | ([CH3CH2CH2CH3])^(-3) H_2 | 9 | 9 | ([H2])^9 C_6H_6 | 2 | 2 | ([C6H6])^2 The equilibrium constant symbol in the concentration basis is: K_c Mulitply the activity expressions to arrive at the K_c expression: Answer: | | K_c = ([CH3CH2CH2CH3])^(-3) ([H2])^9 ([C6H6])^2 = (([H2])^9 ([C6H6])^2)/([CH3CH2CH2CH3])^3
Rate of reaction
![Construct the rate of reaction expression for: CH_3CH_2CH_2CH_3 ⟶ H_2 + C_6H_6 Plan: • Balance the chemical equation. • Determine the stoichiometric numbers. • Assemble the rate term for each chemical species. • Write the rate of reaction expression. Write the balanced chemical equation: 3 CH_3CH_2CH_2CH_3 ⟶ 9 H_2 + 2 C_6H_6 Assign stoichiometric numbers, ν_i, using the stoichiometric coefficients, c_i, from the balanced chemical equation in the following manner: ν_i = -c_i for reactants and ν_i = c_i for products: chemical species | c_i | ν_i CH_3CH_2CH_2CH_3 | 3 | -3 H_2 | 9 | 9 C_6H_6 | 2 | 2 The rate term for each chemical species, B_i, is 1/ν_i(Δ[B_i])/(Δt) where [B_i] is the amount concentration and t is time: chemical species | c_i | ν_i | rate term CH_3CH_2CH_2CH_3 | 3 | -3 | -1/3 (Δ[CH3CH2CH2CH3])/(Δt) H_2 | 9 | 9 | 1/9 (Δ[H2])/(Δt) C_6H_6 | 2 | 2 | 1/2 (Δ[C6H6])/(Δt) (for infinitesimal rate of change, replace Δ with d) Set the rate terms equal to each other to arrive at the rate expression: Answer: | | rate = -1/3 (Δ[CH3CH2CH2CH3])/(Δt) = 1/9 (Δ[H2])/(Δt) = 1/2 (Δ[C6H6])/(Δt) (assuming constant volume and no accumulation of intermediates or side products)](../image_source/71fdfef73e48ff7839b8b6ede8488e6b.png)
Construct the rate of reaction expression for: CH_3CH_2CH_2CH_3 ⟶ H_2 + C_6H_6 Plan: • Balance the chemical equation. • Determine the stoichiometric numbers. • Assemble the rate term for each chemical species. • Write the rate of reaction expression. Write the balanced chemical equation: 3 CH_3CH_2CH_2CH_3 ⟶ 9 H_2 + 2 C_6H_6 Assign stoichiometric numbers, ν_i, using the stoichiometric coefficients, c_i, from the balanced chemical equation in the following manner: ν_i = -c_i for reactants and ν_i = c_i for products: chemical species | c_i | ν_i CH_3CH_2CH_2CH_3 | 3 | -3 H_2 | 9 | 9 C_6H_6 | 2 | 2 The rate term for each chemical species, B_i, is 1/ν_i(Δ[B_i])/(Δt) where [B_i] is the amount concentration and t is time: chemical species | c_i | ν_i | rate term CH_3CH_2CH_2CH_3 | 3 | -3 | -1/3 (Δ[CH3CH2CH2CH3])/(Δt) H_2 | 9 | 9 | 1/9 (Δ[H2])/(Δt) C_6H_6 | 2 | 2 | 1/2 (Δ[C6H6])/(Δt) (for infinitesimal rate of change, replace Δ with d) Set the rate terms equal to each other to arrive at the rate expression: Answer: | | rate = -1/3 (Δ[CH3CH2CH2CH3])/(Δt) = 1/9 (Δ[H2])/(Δt) = 1/2 (Δ[C6H6])/(Δt) (assuming constant volume and no accumulation of intermediates or side products)
Chemical names and formulas
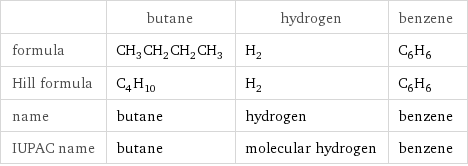
| butane | hydrogen | benzene formula | CH_3CH_2CH_2CH_3 | H_2 | C_6H_6 Hill formula | C_4H_10 | H_2 | C_6H_6 name | butane | hydrogen | benzene IUPAC name | butane | molecular hydrogen | benzene