Input interpretation
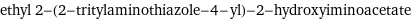
ethyl 2-(2-tritylaminothiazole-4-yl)-2-hydroxyiminoacetate
Basic properties

molar mass | 457.5 g/mol formula | C_26H_23N_3O_3S empirical formula | C_26N_3S_O_3H_23 SMILES identifier | CCOC(=O)C(=NO)C1=CSC(=N1)NC(C2=CC=CC=C2)(C3=CC=CC=C3)C4=CC=CC=C4 InChI identifier | InChI=1/C26H23N3O3S/c1-2-32-24(30)23(29-31)22-18-33-25(27-22)28-26(19-12-6-3-7-13-19, 20-14-8-4-9-15-20)21-16-10-5-11-17-21/h3-18, 31H, 2H2, 1H3, (H, 27, 28)/f/h28H InChI key | KKFBLNMRJSAFAA-UHFFFAOYSA-N
Lewis structure
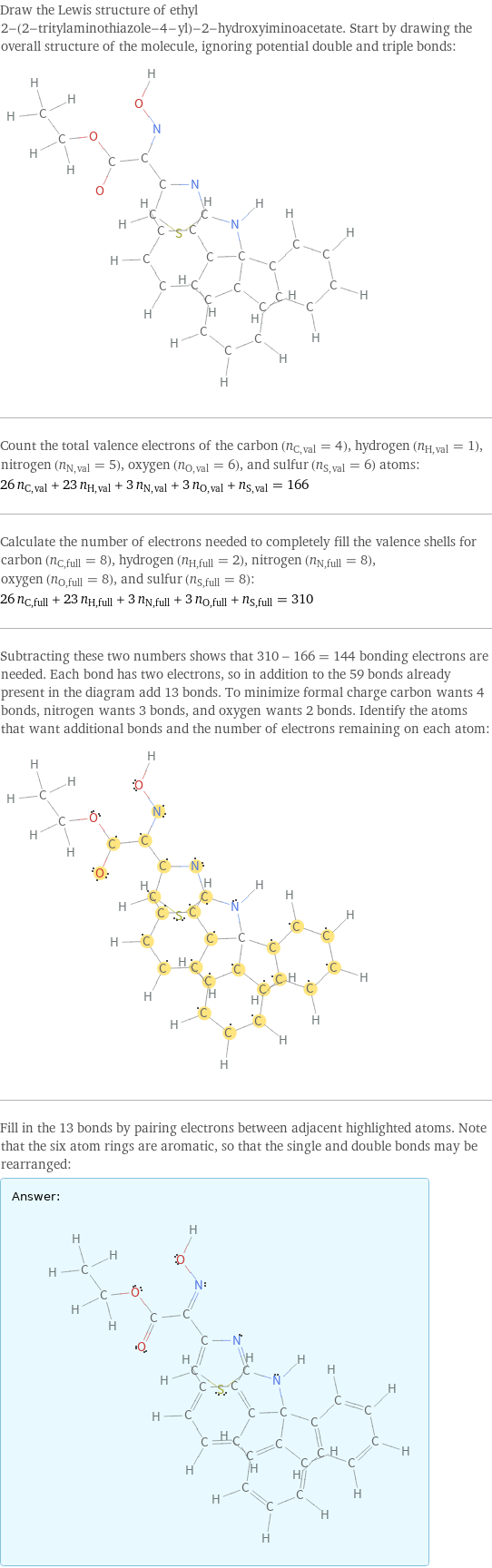
Draw the Lewis structure of ethyl 2-(2-tritylaminothiazole-4-yl)-2-hydroxyiminoacetate. Start by drawing the overall structure of the molecule, ignoring potential double and triple bonds: Count the total valence electrons of the carbon (n_C, val = 4), hydrogen (n_H, val = 1), nitrogen (n_N, val = 5), oxygen (n_O, val = 6), and sulfur (n_S, val = 6) atoms: 26 n_C, val + 23 n_H, val + 3 n_N, val + 3 n_O, val + n_S, val = 166 Calculate the number of electrons needed to completely fill the valence shells for carbon (n_C, full = 8), hydrogen (n_H, full = 2), nitrogen (n_N, full = 8), oxygen (n_O, full = 8), and sulfur (n_S, full = 8): 26 n_C, full + 23 n_H, full + 3 n_N, full + 3 n_O, full + n_S, full = 310 Subtracting these two numbers shows that 310 - 166 = 144 bonding electrons are needed. Each bond has two electrons, so in addition to the 59 bonds already present in the diagram add 13 bonds. To minimize formal charge carbon wants 4 bonds, nitrogen wants 3 bonds, and oxygen wants 2 bonds. Identify the atoms that want additional bonds and the number of electrons remaining on each atom: Fill in the 13 bonds by pairing electrons between adjacent highlighted atoms. Note that the six atom rings are aromatic, so that the single and double bonds may be rearranged: Answer: | |
Estimated thermodynamic properties
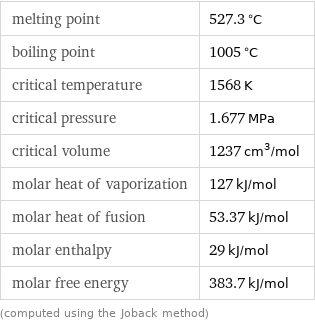
melting point | 527.3 °C boiling point | 1005 °C critical temperature | 1568 K critical pressure | 1.677 MPa critical volume | 1237 cm^3/mol molar heat of vaporization | 127 kJ/mol molar heat of fusion | 53.37 kJ/mol molar enthalpy | 29 kJ/mol molar free energy | 383.7 kJ/mol (computed using the Joback method)
Units

Quantitative molecular descriptors
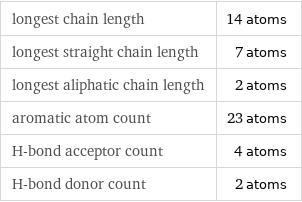
longest chain length | 14 atoms longest straight chain length | 7 atoms longest aliphatic chain length | 2 atoms aromatic atom count | 23 atoms H-bond acceptor count | 4 atoms H-bond donor count | 2 atoms
Elemental composition

Find the elemental composition for ethyl 2-(2-tritylaminothiazole-4-yl)-2-hydroxyiminoacetate in terms of the atom and mass percents: atom percent = N_i/N_atoms × 100% mass percent = (N_im_i)/m × 100% Plan: • Write the chemical formula and gather atomic masses from the periodic table. • Determine values for N_i, m_i, N_atoms and m using these items. • Finally, compute the percents and check the results. Write the chemical formula: C_26H_23N_3O_3S Use the chemical formula to count the number of atoms, N_i, for each element and find the total number of atoms, N_atoms, per molecule: | number of atoms C (carbon) | 26 N (nitrogen) | 3 S (sulfur) | 1 O (oxygen) | 3 H (hydrogen) | 23 N_atoms = 26 + 3 + 1 + 3 + 23 = 56 Divide each N_i by N_atoms to calculate atom fractions. Then use the property that atom fractions must sum to one to check the work: | number of atoms | atom fraction C (carbon) | 26 | 26/56 N (nitrogen) | 3 | 3/56 S (sulfur) | 1 | 1/56 O (oxygen) | 3 | 3/56 H (hydrogen) | 23 | 23/56 Check: 26/56 + 3/56 + 1/56 + 3/56 + 23/56 = 1 Compute atom percents using the atom fractions: | number of atoms | atom percent C (carbon) | 26 | 26/56 × 100% = 46.4% N (nitrogen) | 3 | 3/56 × 100% = 5.36% S (sulfur) | 1 | 1/56 × 100% = 1.79% O (oxygen) | 3 | 3/56 × 100% = 5.36% H (hydrogen) | 23 | 23/56 × 100% = 41.1% Look up the atomic mass, m_i, in unified atomic mass units, u, for each element in the periodic table: | number of atoms | atom percent | atomic mass/u C (carbon) | 26 | 46.4% | 12.011 N (nitrogen) | 3 | 5.36% | 14.007 S (sulfur) | 1 | 1.79% | 32.06 O (oxygen) | 3 | 5.36% | 15.999 H (hydrogen) | 23 | 41.1% | 1.008 Multiply N_i by m_i to compute the mass for each element. Then sum those values to compute the molecular mass, m: | number of atoms | atom percent | atomic mass/u | mass/u C (carbon) | 26 | 46.4% | 12.011 | 26 × 12.011 = 312.286 N (nitrogen) | 3 | 5.36% | 14.007 | 3 × 14.007 = 42.021 S (sulfur) | 1 | 1.79% | 32.06 | 1 × 32.06 = 32.06 O (oxygen) | 3 | 5.36% | 15.999 | 3 × 15.999 = 47.997 H (hydrogen) | 23 | 41.1% | 1.008 | 23 × 1.008 = 23.184 m = 312.286 u + 42.021 u + 32.06 u + 47.997 u + 23.184 u = 457.548 u Divide the mass for each element by m to calculate mass fractions. Then use the property that mass fractions must sum to one to check the work: | number of atoms | atom percent | mass fraction C (carbon) | 26 | 46.4% | 312.286/457.548 N (nitrogen) | 3 | 5.36% | 42.021/457.548 S (sulfur) | 1 | 1.79% | 32.06/457.548 O (oxygen) | 3 | 5.36% | 47.997/457.548 H (hydrogen) | 23 | 41.1% | 23.184/457.548 Check: 312.286/457.548 + 42.021/457.548 + 32.06/457.548 + 47.997/457.548 + 23.184/457.548 = 1 Compute mass percents using the mass fractions: Answer: | | | number of atoms | atom percent | mass percent C (carbon) | 26 | 46.4% | 312.286/457.548 × 100% = 68.25% N (nitrogen) | 3 | 5.36% | 42.021/457.548 × 100% = 9.184% S (sulfur) | 1 | 1.79% | 32.06/457.548 × 100% = 7.007% O (oxygen) | 3 | 5.36% | 47.997/457.548 × 100% = 10.49% H (hydrogen) | 23 | 41.1% | 23.184/457.548 × 100% = 5.067%
Elemental oxidation states

The first step in finding the oxidation states (or oxidation numbers) in ethyl 2-(2-tritylaminothiazole-4-yl)-2-hydroxyiminoacetate is to draw the structure diagram. Next set every oxidation number equal to the atom's formal charge: In ethyl 2-(2-tritylaminothiazole-4-yl)-2-hydroxyiminoacetate hydrogen is not bonded to a metal with lower electronegativity, so it will have an oxidation state of +1. Any element bonded to hydrogen gains the bonding electrons, decreasing their oxidation state by 1 for every bond: With hydrogen out of the way, look at the remaining bonds. There are 5 carbon-nitrogen bonds, 3 carbon-oxygen bonds, 2 carbon-sulfur bonds, 1 nitrogen-oxygen bond, and 25 carbon-carbon bonds. For each of these bonds, assign the bonding electrons to the most electronegative element. First examine the carbon-nitrogen bonds: element | electronegativity (Pauling scale) | C | 2.55 | N | 3.04 | | | Since nitrogen is more electronegative than carbon, the electrons in these bonds will go to nitrogen. Decrease the oxidation number for nitrogen in every highlighted bond (by 1 for single bonds, 2 for double bonds, and 3 for triple bonds), and increase the oxidation number for carbon accordingly: Next look at the carbon-oxygen bonds: element | electronegativity (Pauling scale) | C | 2.55 | O | 3.44 | | | Since oxygen is more electronegative than carbon, the electrons in these bonds will go to oxygen: Next look at the carbon-sulfur bonds: element | electronegativity (Pauling scale) | C | 2.55 | S | 2.58 | | | Since sulfur is more electronegative than carbon, the electrons in these bonds will go to sulfur: Next look at the nitrogen-oxygen bond: element | electronegativity (Pauling scale) | N | 3.04 | O | 3.44 | | | Since oxygen is more electronegative than nitrogen, the electrons in this bond will go to oxygen: Next look at the carbon-carbon bonds: element | electronegativity (Pauling scale) | C | 2.55 | C | 2.55 | | | Since these elements are the same the bonding electrons are shared equally, and there is no change to the oxidation states: Now summarize the results: Answer: | | oxidation state | element | count -3 | C (carbon) | 1 | N (nitrogen) | 2 -2 | O (oxygen) | 3 | S (sulfur) | 1 -1 | C (carbon) | 16 | N (nitrogen) | 1 0 | C (carbon) | 4 +1 | C (carbon) | 2 | H (hydrogen) | 23 +2 | C (carbon) | 1 +3 | C (carbon) | 1 +4 | C (carbon) | 1