molarity of 1 ml of 5 M HCl in 5 L of water

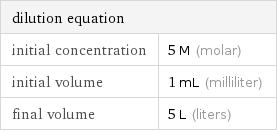
dilution equation | initial concentration | 5 M (molar) initial volume | 1 mL (milliliter) final volume | 5 L (liters)

final concentration | 0.001 M (molar) = 1 mol/m^3 (mole per cubic meter) = 1000 mmol/m^3 (millimoles per cubic meter) = 1 µmol/mL (micromole per milliliter) = 1 mmol/L (millimole per liter) = 1000 µmol/L (micromoles per liter) = 1000 nmol/mL (nanomoles per milliliter) = 0.1 mmol/dL (millimoles per deciliter) = 1 mM (millimolar) = 1000 μM (micromolar)

Calculate the final concentration using the following information: known variables | | V_f | final volume | 5 L V_i | initial volume | 1 mL c_i | initial concentration | 5 M Convert known variables into appropriate units using the following: 1 mL = 0.001 L: 1 M = 1 mol/L: known variables | | V_f | final volume | 5 L V_i | initial volume | 1/1000 L c_i | initial concentration | 5 mol/L The relevant equation that relates final concentration (c_f), final volume (V_f), initial volume (V_i), and initial concentration (c_i) is: c_i V_i = c_f V_f c_i V_i = c_f V_f is equivalent to c_f V_f = c_i V_i: c_f V_f = c_i V_i Divide both sides by V_f: c_f = (c_i V_i)/V_f Substitute known variables into the equation: known variables | | V_f | final volume | 5 L V_i | initial volume | 1/1000 L c_i | initial concentration | 5 mol/L | : c_f = (5 mol/L×0.001 L)/(5 L) Separate the numerical part, (5×0.001)/5, from the unit part, (mol/L L)/L = mol/L: c_f = (5×0.001)/5 mol/L Evaluate (5×0.001)/5: c_f = 0.001 mol/L Convert 0.001 mol/L into M (molar) using the following: 1 mol/L = 1 M: Answer: | | c_f = 0.001 M

c_i V_i = c_f V_f | c_f | final concentration V_f | final volume V_i | initial volume c_i | initial concentration (assuming solutions contain the same chemicals and concentration units)

The amount of solute, n, does not change during a dilution. So the initial amount of solute, n_i, equals the final amount of solute, n_f: n_i = n_f Find an expression for n using the definition of molarity (amount-of-substance concentration): c = n/V c = n/V is equivalent to n/V = c: n/V = c Multiply both sides by V: n = c V Plug the expression for n into n_i = n_f to arrive at the dilution formula: Answer: | | c_i V_i = c_f V_f

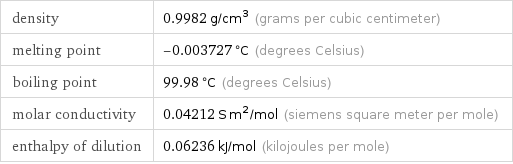
density | 0.9982 g/cm^3 (grams per cubic centimeter) melting point | -0.003727 °C (degrees Celsius) boiling point | 99.98 °C (degrees Celsius) molar conductivity | 0.04212 S m^2/mol (siemens square meter per mole) enthalpy of dilution | 0.06236 kJ/mol (kilojoules per mole)

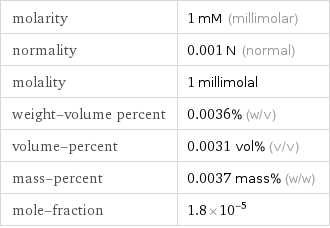
molarity | 1 mM (millimolar) normality | 0.001 N (normal) molality | 1 millimolal weight-volume percent | 0.0036% (w/v) volume-percent | 0.0031 vol% (v/v) mass-percent | 0.0037 mass% (w/w) mole-fraction | 1.8×10^-5