Input interpretation

thin lens equation
Equation

1/i + 1/o = 1/f | i | distance between image and lens o | distance between object and lens f | focal length
Input values

distance between object and lens | 5 meters focal length | 1 meter
Results

distance between image and lens | 125 cm (centimeters) = 4.101 feet = 4' 1.213" = 49.21 inches = 1.25 meters
Possible intermediate steps

Calculate the distance between image and lens using the following information: known variables | | o | distance between object and lens | 5 m f | focal length | 1 m The relevant equation that relates distance between image and lens (i), distance between object and lens (o), and focal length (f) is: 1/i + 1/o = 1/f Bring 1/i + 1/o together using the common denominator i o: (i + o)/(i o) = 1/f Cross multiply: f (i + o) = i o Expand out terms of the left hand side: f i + f o = i o Subtract f o + i o from both sides: i (f - o) = -f o Divide both sides by f - o: i = -(f o)/(f - o) Substitute known variables into the equation: known variables | | o | distance between object and lens | 5 m f | focal length | 1 m | : i = -(1 m×5 m)/(1 m - 5 m) Separate the numerical part, -(1×5)/(1 - 5), from the unit part, (m m)/(m + m) = m: i = -(1×5)/(1 - 5) m Evaluate -(1×5)/(1 - 5): i = 1.25 m Convert 1.25 m into cm (centimeters) using the following: 1 m = 100 cm: Answer: | | i = 125 cm
Ray plot
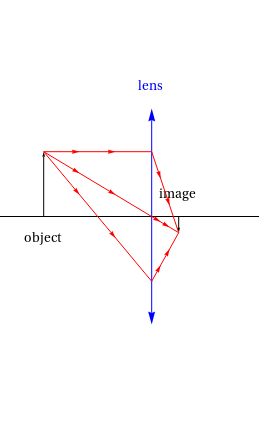
Ray plot