Input interpretation
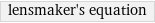
lensmaker's equation
Equation

1/f = (n_l - 1) (1/r_1 - 1/r_2 + ((n_l - 1) d)/(n_l r_1 r_2)) | f | focal length r_1 | radius of curvature for front surface of lens r_2 | radius of curvature for back surface of lens d | lens thickness n_l | refractive index of lens material (signs for radius of curvature are positive/negative (negative/positive) if the front (back) surface of lens is convex/concave)
Input values

radius of curvature for front surface of lens | 300 cm (centimeters) radius of curvature for back surface of lens | -300 cm (centimeters) lens thickness | 5 mm (millimeters) refractive index of lens material | 1.5
Results

focal length | 3.001 meters = 9.845 feet = 9' 10.14" = 118.1 inches = 3.282 yards = 300.1 cm (centimeters)
Possible intermediate steps

Calculate the focal length using the following information: known variables | | r_1 | radius of curvature for front surface of lens | 300 cm r_2 | radius of curvature for back surface of lens | -300 cm d | lens thickness | 5 mm n_l | refractive index of lens material | 1.5 Convert known variables into appropriate units using the following: 1 cm = 0.01 m: 1 cm = 0.01 m: 1 mm = 0.001 m: known variables | | r_1 | radius of curvature for front surface of lens | 3 m r_2 | radius of curvature for back surface of lens | -3 m d | lens thickness | 1/200 m n_l | refractive index of lens material | 1.5 The relevant equation that relates focal length (f), radius of curvature for front surface of lens (r_1), radius of curvature for back surface of lens (r_2), lens thickness (d), and refractive index of lens material (n_l) is: 1/f = (n_l - 1) (1/r_1 - 1/r_2 + ((n_l - 1) d)/(n_l r_1 r_2)) Take the reciprocal of both sides: f = 1/((-1 + n_l) (1/r_1 - 1/r_2 + (d (-1 + n_l))/(n_l r_1 r_2))) Substitute known variables into the equation: known variables | | r_1 | radius of curvature for front surface of lens | 3 m r_2 | radius of curvature for back surface of lens | -3 m d | lens thickness | 1/200 m n_l | refractive index of lens material | 1.5 | : f = 1/((-1 + 1.5) (1/(3 m) - 1/(-3 m) + (0.005 m (-1 + 1.5))/(1.5×3 m×-3 m))) Separate the numerical part, 1/((-1 + 1.5) (1/3 - 1/(-3) + (0.005 (-1 + 1.5))/(1.5×3×-3))), from the unit part, 1/(1/m + 1/m + m/(m m)) = m: f = 1/((-1 + 1.5) (1/3 - 1/(-3) + (0.005 (-1 + 1.5))/(1.5×3×-3))) m Evaluate 1/((-1 + 1.5) (1/3 - 1/(-3) + (0.005 (-1 + 1.5))/(1.5×3×-3))): Answer: | | f = 3.001 m