Input interpretation
1 cm^3 of hydrogen bromide
Basic properties for 1 cm^3
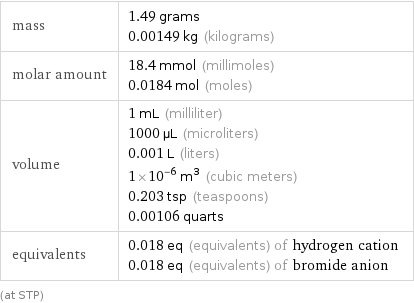
mass | 1.49 grams 0.00149 kg (kilograms) molar amount | 18.4 mmol (millimoles) 0.0184 mol (moles) volume | 1 mL (milliliter) 1000 µL (microliters) 0.001 L (liters) 1×10^-6 m^3 (cubic meters) 0.203 tsp (teaspoons) 0.00106 quarts equivalents | 0.018 eq (equivalents) of hydrogen cation 0.018 eq (equivalents) of bromide anion (at STP)
Corresponding quantities
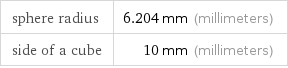
sphere radius | 6.204 mm (millimeters) side of a cube | 10 mm (millimeters)
Thermodynamic properties for 1 cm^3

heat of solution Δ_solH° | -1.568 kJ (kilojoules)
Mass composition for 1 cm^3
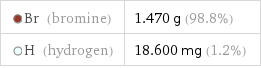
Br (bromine) | 1.470 g (98.8%) H (hydrogen) | 18.600 mg (1.2%)

Mass composition for 1 cm^3
Lewis structure

Draw the Lewis structure of hydrogen bromide. Start by drawing the overall structure of the molecule: Count the total valence electrons of the bromine (n_Br, val = 7) and hydrogen (n_H, val = 1) atoms: n_Br, val + n_H, val = 8 Calculate the number of electrons needed to completely fill the valence shells for bromine (n_Br, full = 8) and hydrogen (n_H, full = 2): n_Br, full + n_H, full = 10 Subtracting these two numbers shows that 10 - 8 = 2 bonding electrons are needed. Each bond has two electrons, so the above diagram has all the necessary bonds. There is 1 bond and hence 2 bonding electrons in the diagram. Lastly, fill in the remaining unbonded electrons on each atom. In total, there remain 8 - 2 = 6 electrons left to draw: Answer: | |
Chemical names and formulas

formula | HBr Hill formula | BrH name | hydrogen bromide IUPAC name | hydrogen bromide
Substance properties

molar mass | 80.912 g/mol phase | gas (at STP) melting point | -86.8 °C boiling point | -66.38 °C density | 0.003307 g/cm^3 (at 25 °C) solubility in water | miscible surface tension | 0.0271 N/m dynamic viscosity | 8.4×10^-4 Pa s (at -75 °C)
Units
